1 堆 Heap - 最小堆&最大堆

1.1 简介

堆(heap) 的实现是一种基于树的特殊的数据结构，它可以在数组上构建出树的结构体，并满足堆的属性

最小堆：如果P 是 C 的一个父级节点，那么 P 的key(或value)应小于或等于 C 的对应值
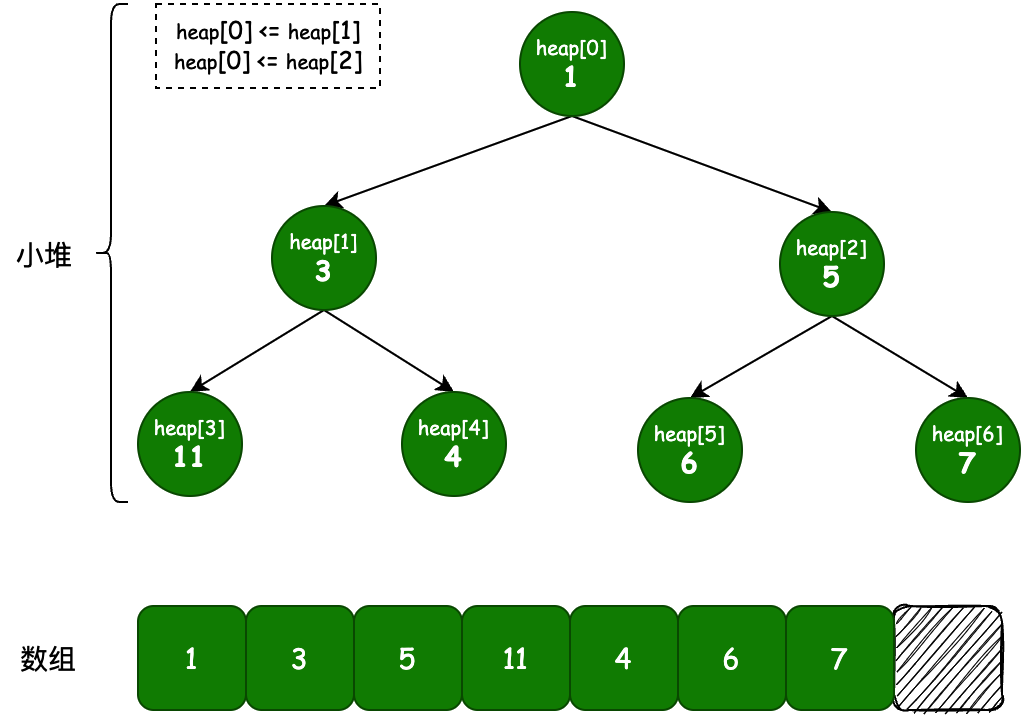
最大堆：与最小堆的定义正好相反，最大堆(max heap) , P 的key(或value)大于 C 的对应值

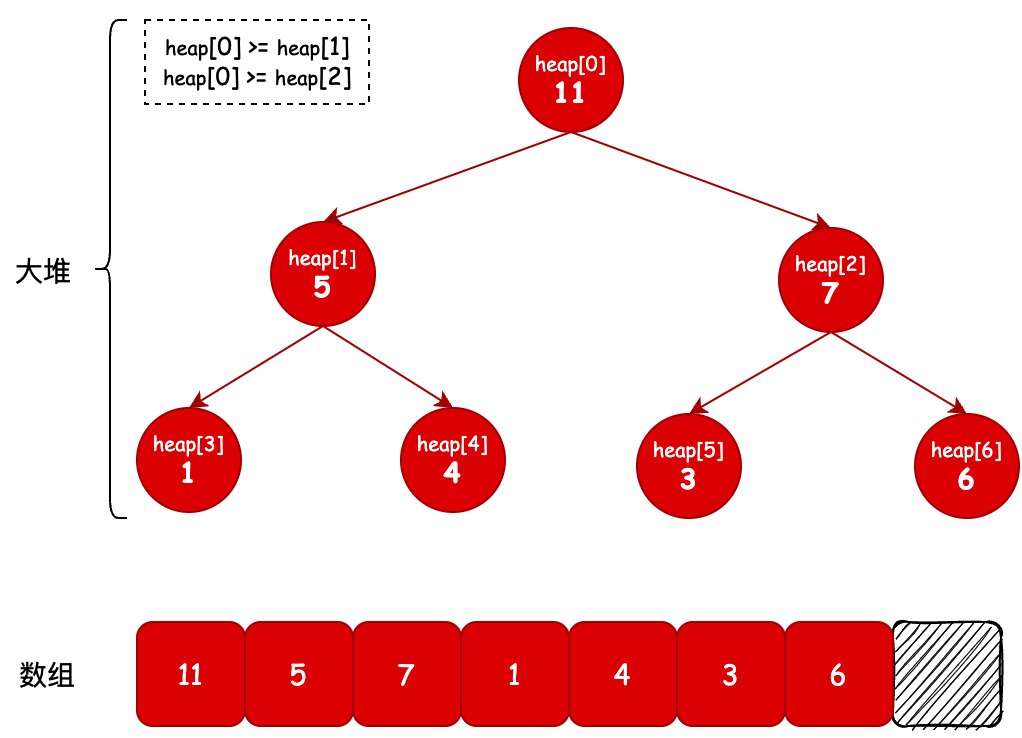
1.2 实现

堆的实现在 Java API 中主要体现在延迟队列的实现二叉堆上
从对堆的数据结构介绍上可以看到，小堆和大堆的唯一区别仅是对元素的排序方式不同。所以也就是说在存放和获取元素的时候对元素的填充和摘除时，排序方式不同而已

1.2.1 入堆

堆的在存放元素时，以遵循它的特点，会在存放过程中，通过队尾元素向上比对迁移

private void siftUpComparable(int k, E x) {
    logger.info("【入队】元素：{} 当前队列：{}", JSON.toJSONString(x), JSON.toJSONString(queue));
    while (k > 0) {
        // 获取父节点Idx，相当于除以2
        int parent = (k - 1) >>> 1;
        logger.info("【入队】寻找当前节点的父节点位置。k：{} parent：{}", k, parent);
        Object e = queue[parent];
        // 如果当前位置元素，大于父节点元素，则退出循环
        if (compareTo(x, (E) e) >= 0) {
            logger.info("【入队】值比对，父节点：{} 目标节点：{}", JSON.toJSONString(e), JSON.toJSONString(x));
            break;
        }
        // 相反父节点位置大于当前位置元素，则进行替换
        logger.info("【入队】替换过程，父子节点位置替换，继续循环。父节点值：{} 存放到位置：{}", JSON.toJSONString(e), k);
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
    logger.info("【入队】完成 Idx：{} Val：{} \r\n当前队列：{} \r\n", k, JSON.toJSONString(x), JSON.toJSONString(queue));
}

入堆的实现 add 方法最终会调用到 siftUpComparable 方法，进行排序的方式进行处理。而这个排序 compareTo 方法是由具体的 MinHeap、MaxHeap 来做实现
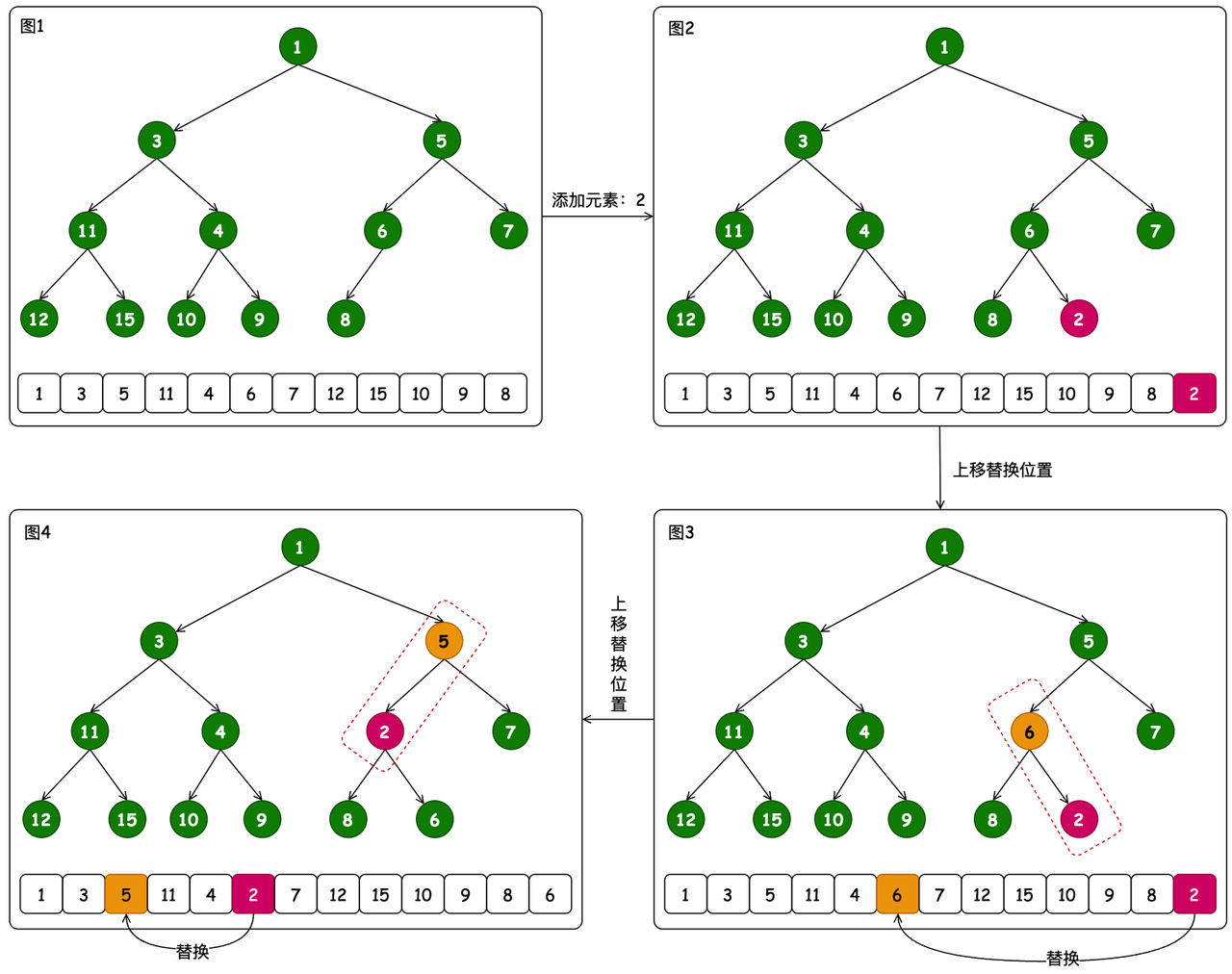
首先将元素2挂到队列尾部，之后通过 (k - 1) >>> 1 计算父节点位置，与对应元素进行比对和判断交换
交换过程包括 2->6、2->5，以此交换结束后元素保存完毕

1.2.2 出堆实现

出堆只要把根元素直接删除弹出即可。接下来需要在根元素迁移走后，寻找另外的最小元素迁移到对头。这个过程与入堆正好相反，这是一个不断向下迁移的过程

private void siftDownComparable(int k, E x) {
    // 先找出中间件节点
    int half = size >>> 1;
    while (k < half) {
        // 找到左子节点和右子节点，两个节点进行比较，找出最大的值
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        // 左子节点与右子节点比较，取最小的节点
        if (right < size && compareTo((E) c, (E) queue[right]) > 0) {
            logger.info("【出队】左右子节点比对，获取最小值。left：{} right：{}", JSON.toJSONString(c), JSON.toJSONString(queue[right]));
            c = queue[child = right];
        }
        // 目标值与c比较，当目标值小于c值，退出循环。说明此时目标值所在位置适合，迁移完成。
        if (compareTo(x, (E) c) <= 0) {
            break;
        }
        // 目标值小于c值，位置替换，继续比较
        logger.info("【出队】替换过程，节点的值比对。上节点：{} 下节点：{} 位置替换", JSON.toJSONString(queue[k]), JSON.toJSONString(c));
        queue[k] = c;
        k = child;
    }
    // 把目标值放到对应位置
    logger.info("【出队】替换结果，最终更换位置。Idx：{} Val：{}", k, JSON.toJSONString(x));
    queue[k] = x;
}

不断地向下迁移元素。这个过程会比对左右子节点的值，找到最小的

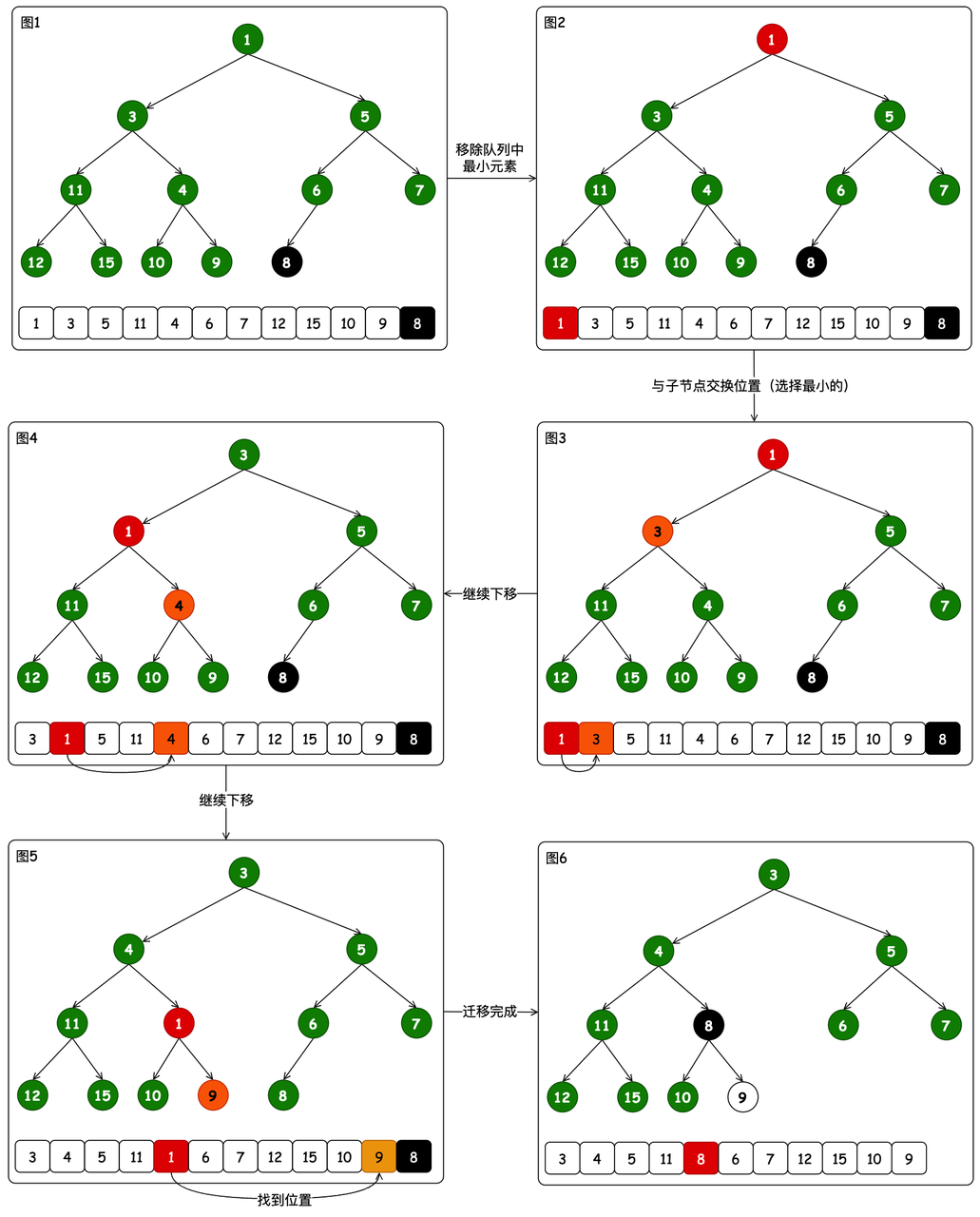
这里以弹出元素1举例，之后将堆尾元素替换到相应的位置。整个过程分为6张图表述。

图1到图2，找出根元素弹出。

图3到图4，将根元素向下迁移，与子元素比对，并替换位置。如果这个位置与8相比，小于8则继续向下迁移

图4到图5，继续迁移，在原节点4的位置对应的两个子元素，都比8大，这个时候就可以停下来了

图5到图6，更换元素位置，把队尾的元素替换到对应元素1向下迁移检测的位置

1.2.3 小堆实现

小堆是一个正序比对

public class MinHeap extends Heap<Integer> {

    @Override
    public int compareTo(Integer firstElement, Integer secondElement) {
        return firstElement.compareTo(secondElement);
    }

}

测试

@Test
public void test_min_heap() {
    MinHeap heap = new MinHeap();
    // 存入元素
    heap.add(1);
    heap.add(3);
    heap.add(5);
    heap.add(11);
    heap.add(4);
    heap.add(6);
    heap.add(7);
    heap.add(12);
    heap.add(15);
    heap.add(10);
    heap.add(9);
    heap.add(8);
    // 弹出元素
    while (heap.peek() != null){
        logger.info("测试结果：{}", heap.poll());
    }
}

小堆就是一个正序的输出结果，从小到大的排序和输出
小堆空间：[1,3,5,11,4,6,7,12,15,10,9,8,null,null,null,null,null,null,null,null,null,null,null,null]

1.2.4 大堆实现

大堆是一个反序比对

public class MaxHeap extends Heap<Integer> {

    @Override
    public int compareTo(Integer firstElement, Integer secondElement) {
        return secondElement.compareTo(firstElement);
    }

}

测试

@Test
public void test_max_heap() {
    MaxHeap heap = new MaxHeap();
    // 存入元素
    heap.add(1);
    heap.add(3);
    heap.add(5);
    heap.add(11);
    heap.add(4);
    heap.add(6);
    heap.add(7);
    heap.add(12);
    heap.add(15);
    heap.add(10);
    heap.add(9);
    heap.add(8);
    // 弹出元素
    while (heap.peek() != null){
        logger.info("测试结果：{}", heap.poll());
    }
}

大堆就是一个反序的输出结果，从大到小的排序和输出
大堆空间： [15,12,8,11,10,7,6,1,5,4,9,3,null,null,null,null,null,null,null,null,null,null,null,null]

1.3 常见面试题

堆的数据结构是什么样？
- 是一种基于树的特殊的数据结构，堆的实现在 Java API 中主要体现在延迟队列的实现二叉堆上
堆的数据结构使用场景？
- 堆排序
- 优先队列
- 图像处理：用来存储中心点，并计算其他像素和中心点之间的距离。这种计算可以被用来对像素进行分组或图像分割等过程
- 内存管理：用来进行内存的分配和释放
- 网络：网络路由算法中，可以使用堆数据结构来计算最短路径，以及路由器队列管理、流量控制等等
堆的数据结构实现方式有哪些？
- 二叉堆：本质上是一种完全二叉树，分为两类：最大堆和最小堆
  - 最大堆的任何一个父节点的值都大于或等于左右子节点的值
  - 最小堆的任何一个父节点的值都小于或等一它左右子节点的值
- 二项堆（binomial heap）：一种类似于二叉堆的堆结构。与二叉堆相比，其优势是可以快速合并两个堆，因此它属于可合并堆（mergeable heap）抽象数据类型的一种
- 斐波那契堆(Fibonacci heap)：和二项堆一样，也是一种可合并堆；可用于实现合并优先队列
最小堆和最大堆的区别是什么？
- 最大堆的任何一个父节点的值都大于或等于左右子节点的值
- 最小堆的任何一个父节点的值都小于或等一它左右子节点的值
有了解斐波那契堆吗？
- 斐波那契堆(Fibonacci heap)是堆中一种，可用于实现合并优先队列
- 斐波那契堆比二项堆具有更好的平摊分析性能，合并操作的时间复杂度是O(1)
- 与二项堆一样，也是由一组堆最小有序树组成，并且是一种可合并堆
- 与二项堆不同的是，斐波那契堆中的树不一定是二项树，而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的

Breeze Blog

java数据结构【树形】 - 堆 Heap-最小堆&最大堆